I’ve used the Great Circle Mapper website (GCMap.com) for a couple years and found it useful to plot my itineraries and get some basic distance information. However, I’ve never really understood all the cool features that some others like to use. I set out last weekend to teach myself more about it.
First, a Cartography Lesson
It helps if you already know the definition of a “great circle.” From Wikipedia:
For any two points on a sphere, there is a great circle through the two points. The minor arc of the great circle is the shortest surface path between them. It makes perfect sense when you look at a round globe and try to connect two points.
A great circle divides a sphere into two equal halves. The equator is an example of a great circle. Any two points (or cities) on a circle can be used to divide it into two arcs, or curved lines. If your points are directly opposite each other, then the arcs are equal, but usually one will be shorter than the other.

So why does the shortest distance between two cities look like it’s taking a curved detour instead of a straight line?
When you look at most maps of Earth, someone has taken a round surface and found some way to warp it to fit on a flat piece of paper or screen. The most common one you’ll see on GCMap.com or elsewhere is an equirectangular projection, or plate carrée, which stretches out the poles so that they are just as long as the equator (e.g., Greenland looks as big as the continental United States).
Of course, this is absurd because the equator is roughly 25,000 miles long and the poles are individual points. But because paper is rectangular and most people don’t live at the poles, it works out as long as you don’t use it to represent what things actually look like. All maps face this challenge between representing reality and providing useful navigational information. Highly stylized subway maps are a good example.
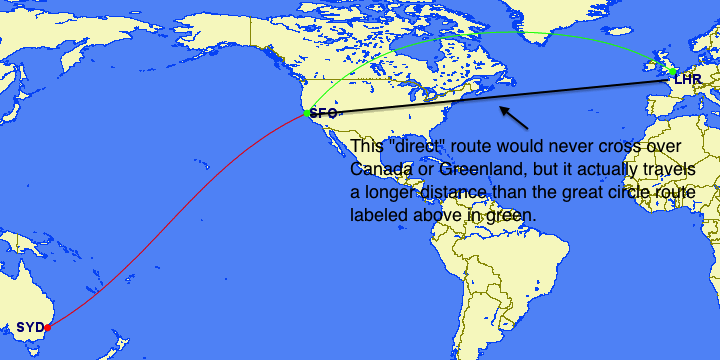
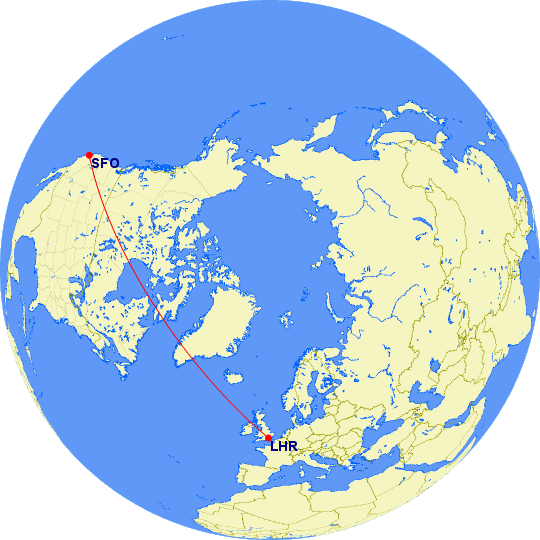
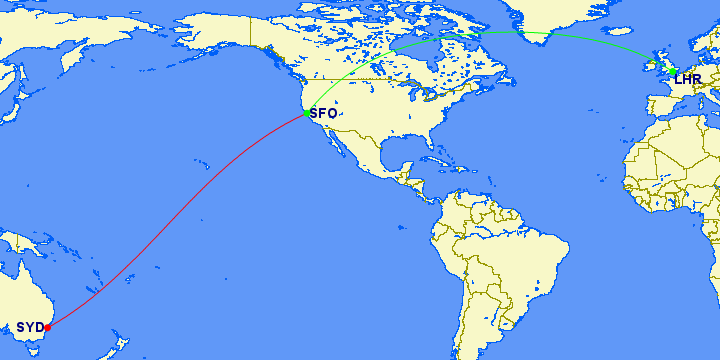
Let’s get back to the great circle. Because we have taken the shortest distance on a round surface and are now tracing that route on a flat, distorted map, the line will also look distorted. It creates the sinusoidal curves you notice when crossing between hemispheres from San Francisco to Sydney and explains why the shortest distance from San Francisco to London involves a large arc near the pole over Canada and Greenland.
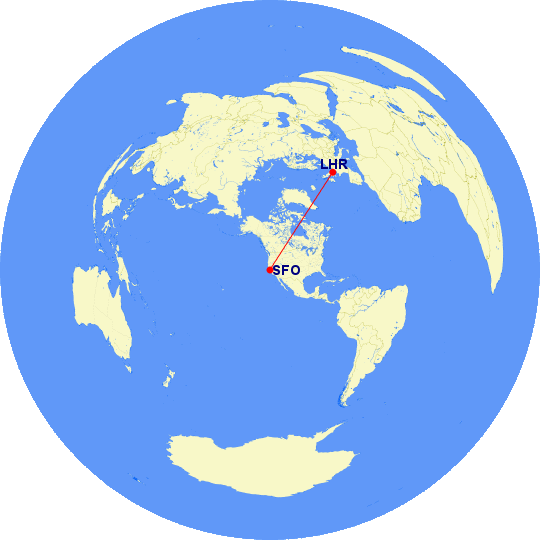
There are three other map styles to choose from on GCMap.com. Orthographic maps are round and represent what Earth would look like if you were in space looking back. You won’t be able to see the far half of the planet, and the edges will appear distorted. For extreme polar routes, you’ll sometimes be shown a polar orthographic projection because the equirectangular map would just have a long line running along the top or bottom. It’s accurate but not especially helpful. You can also choose a standard orthographic projection as if you were looking at the equator.
Finally, the azimuthal equidistant projection is also round but attempts to show the entire globe. By default it centers on your airport of origination but has extreme distortions at the edges; I’ve never found it useful. It might help in cases where you need a circular map (e.g., drawing a radius) but some destinations are too far away to be visible on an orthographic projection. Wikipedia has a good description of several other types of projections if, like me, you find this stuff fascinating. 😛
Commands and Tricks
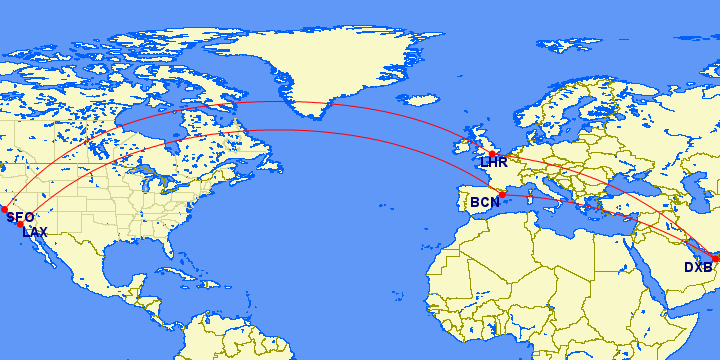
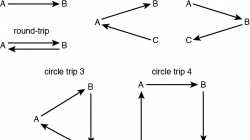
To draw a route between two airports, such as SFO and LHR, just connect them with a hyphen. To draw a continuing route from one city to another (or just a round-trip) continue adding airports with hyphens between them. Example:
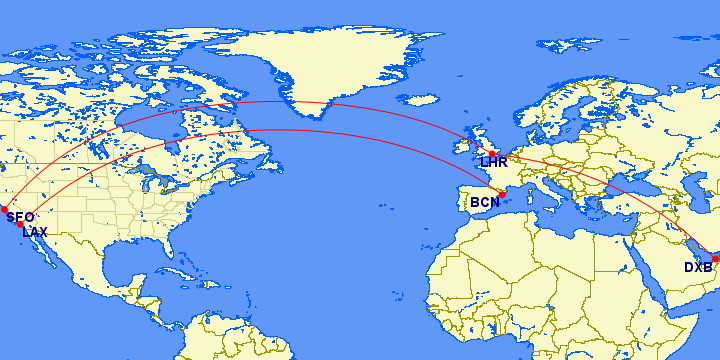
SFO-LHR-DXB-BCN-LAX-SFO
To draw multiple routes, not necessarily connecting from one airport to another, use commas. Example:
SFO-LHR-DXB,BCN-LAX-SFO
Two of the easiest uses of this feature are to plot a map of your itinerary and to get the distance of individual segments (when estimating how many miles you’ll earn). You’ve already seen examples of the maps above. The distance information will appear below along with some other navigational details.
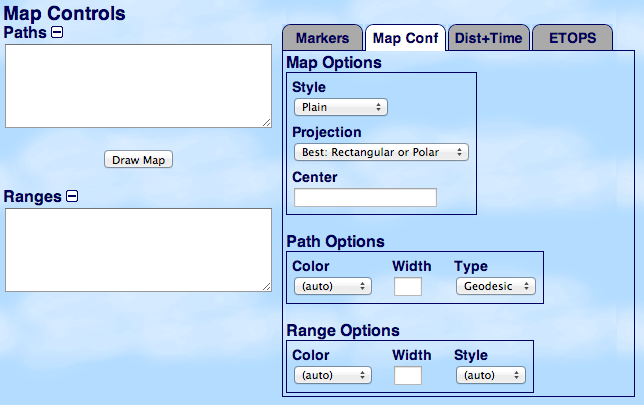
Lots more can be done with the map using the Map Controls panel at the bottom. However, it’s often easier to just learn the text commands and do it yourself the first time.
You can add color to different routes on your map. The default color is red. If you wish to use a different color — or multiple colors — you can specify the color easily. There are two options. First, write “color:red” or “c:red” before the route you want to change with a comma between them. Change the word “red” to whatever color you prefer. For example:
SFO-SYD,color:green,SFO-LHR
This will display San Francisco to Sydney in the default color, which is red. Then the color is changed to green, which will apply to the next route from San Francisco to London. You can change the color multiple times.
You can specify a range using the “@” symbol. The default unit is nautical miles (nm) unless some other unit is specified. Options include nautical miles (nm), statute miles (mi), kilometers (km), or minutes (min) at 389 knots. This example is for distances between 500 miles and 1,000 miles of San Francisco:
500mi,1000mi@SFO
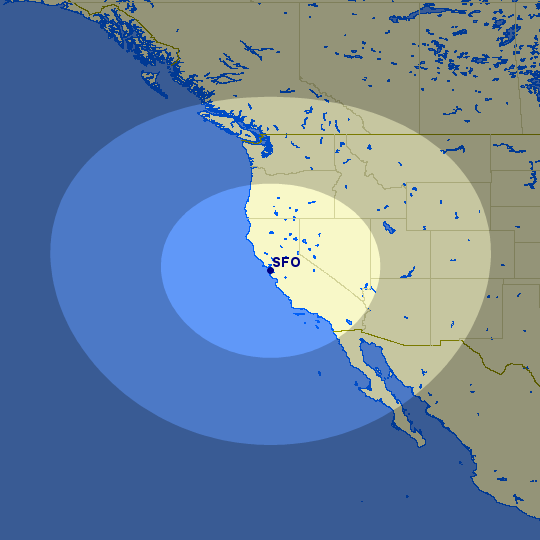
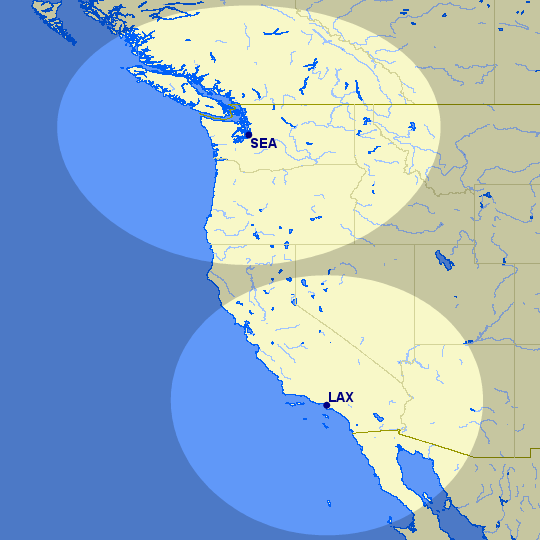
Amol made especially good use of this when he was talking about using open jaws to maximize the value of Delta SkyMiles redemptions. You can also specify the area around one or more airports. This example shows the area within one hour of Seattle and Los Angeles (notice how the bubble around Seattle is more distorted as a consequence of the equirectangular projection):
60min@(SEA,LAX)
One practical use of this feature involves the ETOPS rating, which allows a twin-engine aircraft to travel further from nearby airports that it might need to divert to if one of those engines failed en route. Normally this range is 60 minutes, and ETOPS allows a craft to fly between 90 and 180 minutes from the nearest alternative airport. The Wandering Aramean made good use of this tool to plot routes that the Boeing 787 could still fly without an ETOPS rating.
Finally, remember that you should give attribution to GCMap.com when you use and share your maps elsewhere. I haven’t always been great about including a link, but I do try to remember GCMap.com. You can learn more here.
Maps generated by the Great Circle Mapper – copyright © Karl L. Swartz.